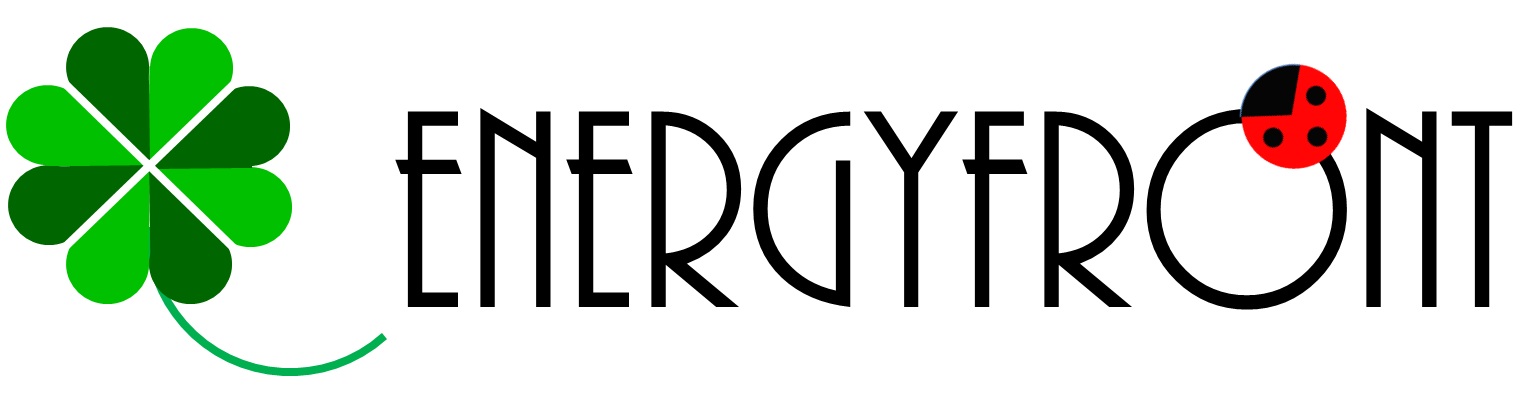その3 量子力学からみた電子軌道
前回は電子と原子核が電荷を帯びた粒だとして、古典力学から見ると原子は不思議だらけであることを示しました。今回は、量子力学にとっての「あたりまえ」の視点から原子を見ていきたいと思います。前回述べた原子の中の電子の謎を一気に解決するため難しく感じる方も多いと思います。
その場合は軽く読み飛ばして量子力学に慣れた頃にまた読み直すと良いと思います。運動量、エネルギー、波長、周波数という概念については知っている前提でお話します。
1. 粒は波の中にいる
古典力学では粒だと思われてきた原子核や電子は、量子力学では波の中に見つかります。逆に光など古典力学では波だと思われてきたものも捕まえてみると粒だということもわかりました。粒は波の姿をもち、波は粒の姿を持っていることがわかったのでした。
しかし粒と波というのは普通の感覚ではかなり違うものです。粒とは、古典力学では位置と速度が分かればその動きの全てが分かる、一本の線で描ける軌道を進む存在です。
一方、波は多数の粒子が集まった媒質の中の振動が、波源から全方向に伝播していくものとして古典力学では考えられてきました。

前者は一つの粒子が実際に進むイメージで、後者は媒質は移動せずその動きだけが色々な方向に伝わるイメージです。
こういう全く異なる性質の概念が結びつくのはやはり奇妙なことです。量子力学における波は、ひとつの粒がそれぞれにもつ波で、私たちが日常生活で見たことのある波とはかなり異なるものです。
まず言っておきたいのは、量子力学の波が本当のところ一体何であるのかについては現在まで誰も知らないということです。それゆえ、奇妙さはこの話を聞いた後も消えることはないでしょう。しかしその波に基づいて全ての議論が進みます。
量子力学の波と粒の関係の本質を書き出すと次のようになります。「私たちが電子を見つける時にはいつでも粒として見つかる。見つかりやすい場所とそうでない場所があり、その確率が波の形をしている」というものです。
粗っぽい譬えをするならば、分身の術を行っている忍者が作る多数の濃淡のある残像が量子力学の波に相当します。濃い残像に石をぶつけると忍者が捕まる確率が高いと言えます。そして足を止めた時に全ての残像は消え、一人だけになる感じです。動いている時に波があり、止まると波は消えます。

仮に分身の術では動きの早い場所では見えず遅い場所では見えるようにして残像を作っているのだとすると、一歩を動かす歩幅(ストライド)や周波数(ピッチ)と残像は関係します。波には波長と周波数がありその点では似ています。
2. 粒子の運動の激しさと波長には関係がある
粒が動いている時には波があるわけですが、運動する電子がどんな波でも作れるかというとそうではありません。
運動量によって波長が決まります。具体的な数式についてはまた別の回に紹介しますが、運動量が大きいほど波長は短くなります。この性質を利用したものとして電子顕微鏡があります。虫眼鏡や顕微鏡などでは、波長より小さいものは見えません。人間の目で見える範囲の光の波長では微生物を見るのが限界ですが、電子顕微鏡ではもっと短い波長にすることで原子レベルまで見ることができます。
3. 速度と位置を同時に知ることはできない
動いている電子は波の中にいます。運動量やエネルギーははっきりしていますが波の中のどこにいるのかはわかりません。(もう一度忍者の分身を思い出してください。多数の分身が見えている間は各瞬間に移り変わりどこにいるかを言いにくい状況です)。
観測して粒として見つけたとき、場所がはっきりします。しかしこの瞬間に運動は止まってしまったわけなので波は失われます。
このように波(運動量)がある時には粒(位置)の情報はなく、粒(位置)がある時には波(運動量)の情報はありません。このように、古典力学では当たり前だった位置と運動量を同時に知ることは量子力学ではできません。これを「不確定性原理」と言います。これは人間が知らないだけで客観的には決まっている、あるいは神様は知っている、というものではなく、本当に決まっていないと考えるのが正しいです。今後量子力学の波について深めていく時にまたご紹介します。
不確定性原理は原子核と電子がくっついて潰れてしまわない理由の一つでもあります。仮に外から押して電子が原子核に接近し原子が潰れそうになったとします。不確定性原理により、電子の位置は原子核に近い場所に押しつけられて位置が確定しそうになる反動として、運動の不確定さが非常に大きくなります。つまり大きなエネルギーで押し返すことになります。
4. 閉じ込められたとき定在波になる
ここでキーワードの一つとなる共鳴について説明します。
音とは空気の疎密振動の波です。音階とは周波数で決まります。笛やギターなどでは空気や弦の振動範囲を変えることで決まった音を出しますね。
本来、空気や弦は色々な振動が可能で、いろいろな振動数の波を伝えることができるのですが、これらの楽器では波を伝える範囲を制限することにより、ある決まった振動しかできなくなることを利用しています。
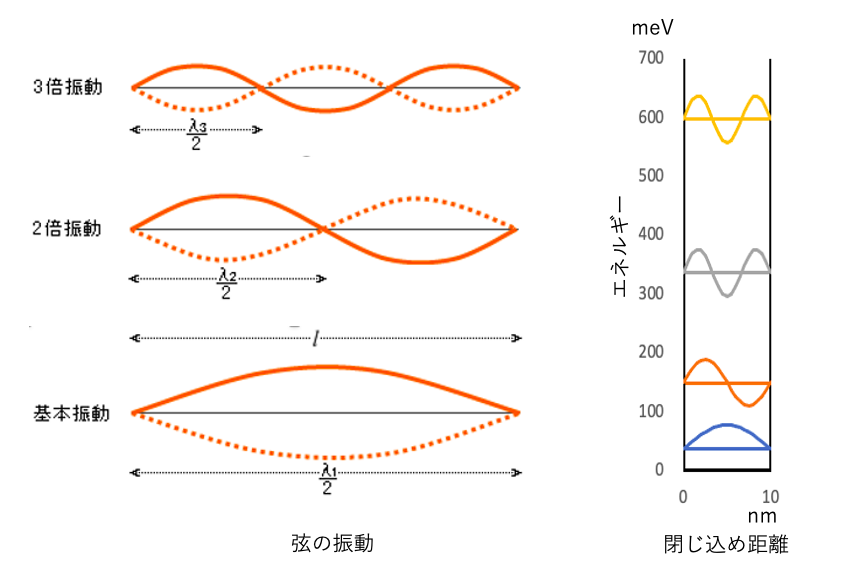
この現象は共鳴と呼ばれています。共鳴とは反射やループによって元の場所に帰ってきた波が元の波ときっちり重なる現象です。きっちり重なる波以外は消しあってしまい消えてしまいますが、きっちり重なる特定の波長や周期の波だけが残ります。この時、波は動かずその場で振動するように見えます(定在波と言います)。
なお、きっちり重なる波はただ一つだけではなく、例えば1/2, 1/3の波長の音など複数可能です。笛でも弦でも複数の許される共鳴音が重なっていることが普通です。
量子力学の波も閉じ込められたときに共鳴します。この状況を原子の場合についてお話しします。
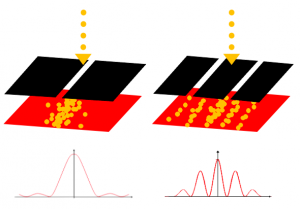
正帯電の原子核に負帯電の電子が引きつけられている状況は、下の図のように静電気のエネルギーの壁で閉じ込められている状況と言い換えることができます。
量子力学の場合も閉じ込められた波は定在波だけが生き残りますから、この場合もいくつかの許される定在波が決まります。
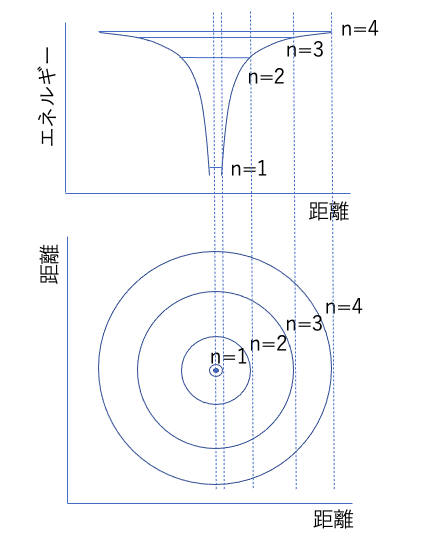
この量子力学の波の定在波こそが原子中の電子の軌道なのです。以前に示した原子内の電子軌道はこの定在波をエネルギーの低い順に並べたものです。
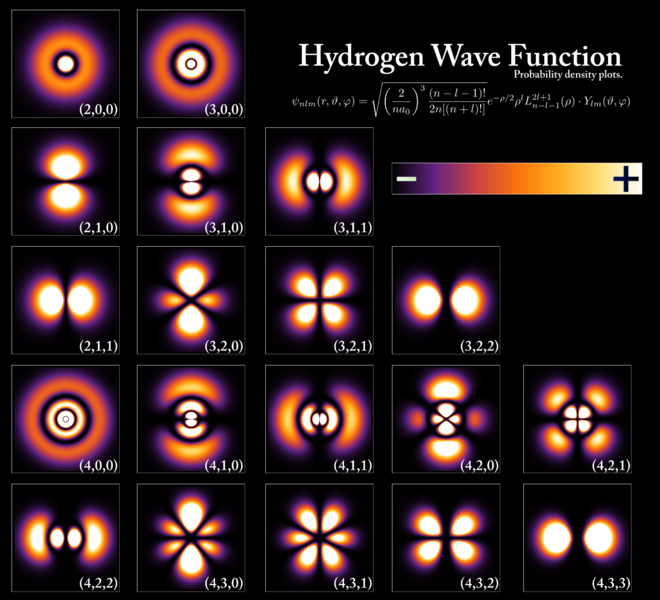
軌道にいる電子はエネルギーと運動量が決まった状態にあります。不確定性原理により、私たちは軌道のどこに電子がいるのかを知ることはできません。
上の図のように3次元の閉じ込めの中での共鳴波として生じる電子軌道は立体構造を持っています。
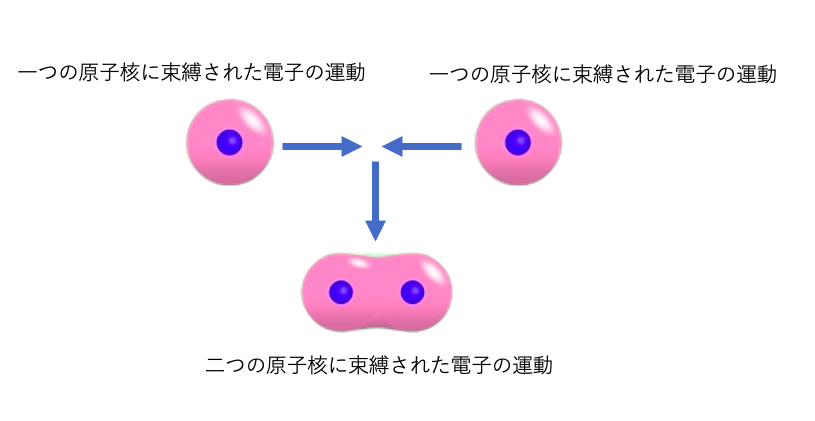
また、一つの電子が二つの原子核の静電気力に引かれるとき、二つの原子をつなぐ閉じ込められた定在波(分子軌道)の中にいることになります。これが化学結合の正体です。分子が幾何学的な配置を取るのも立体的な軌道のためです。
5. 電子は軌道を移るときだけ光を照射・吸収する
電子が出す光がSpring-8の場合と原子の場合で違う理由について説明します。まず原子の光のスペクトルが「とびとびの決まった波長のスペクトル」だけになるかを述べます。
ズバリ答えから言うと、共鳴した軌道(定在波)にいる電子は安定で光を出し入れしません。一方、ある軌道から別の軌道に移る(遷移と言います)場合には光が出し入れされます。出し入れされる光はきっちりそのエネルギー差となります。
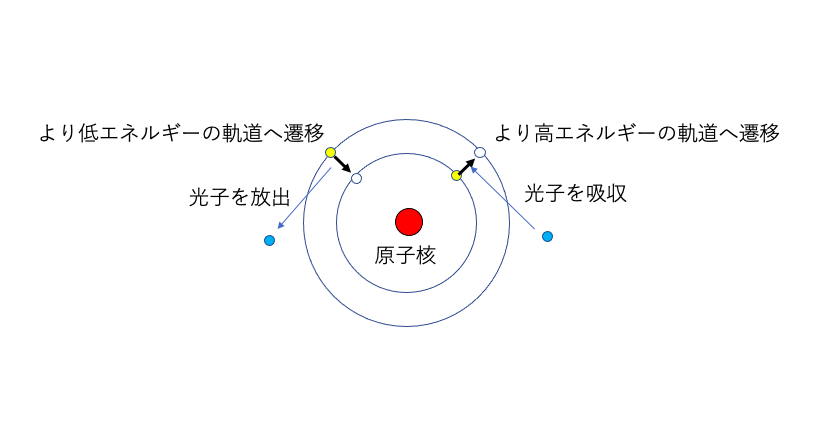
なぜそうなのか?に残念ながら答えることはできません。波についての明確な説明がないまま法則が述べられ、もどかしさがあることと思います。しかしこれが現在言える精一杯のところで、私たちにわかるのは実験で確認されたそのような法則があり、そう考えると上手くいくということだけです。量子力学の波が一体何なのかが明らかでない以上、なぜそうなのかを誰もが納得できる形で答えることは残念ながらできません。
定在波である電子軌道は光の出入りがない安定状態であることだけが事実です。
6. 自由に動ける電子は波束の中にいる
次に古典的な電子の運動は光を放出することを説明します(前回紹介したSPring-8で動く電子は粒として動き光を放出するのでした)。
原子の中の電子との違いは、それが原子核と違って狭い空間に閉じ込められていないことです。電子の閉じ込めを弱くしていくとどうなるかを考えましょう。
閉じ込めの空間をどんどん広げて行くと、共鳴状態のエネルギー(エネルギー準位と言います)の間隔はどんどん狭くなり、やがてほぼ連続になります。電子は決まったエネルギーしか許されなかった状態から、連続したエネルギーを自由に選べるようになります。つまり空間的に閉じ込めがなくなると電子は位置だけでなくエネルギーも自由な値を取れるようになります。
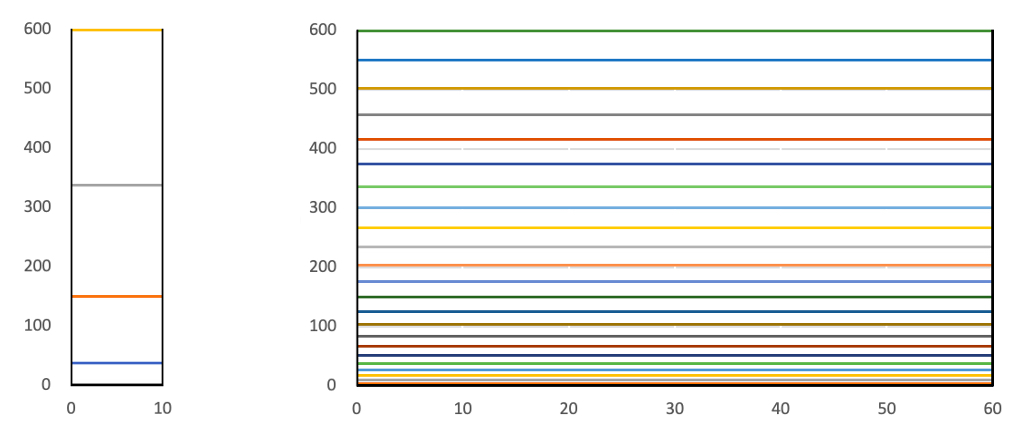
すると電子は一つの軌道だけでなく近くのエネルギー準位に簡単に移ります。複数のエネルギー準位を行ったり来たりということもできます。
それぞれのエネルギーではそれぞれの波長を持ちますから、複数のエネルギーをとることは複数の波が重なった状態となると考えることができます。
このように少し波長が異なる波が重なり合っているとき、波束と呼ばれる「こぶ」ができます。音波が重なった場合の「うなり」に相当します。
従って束縛のない自由な空間では電子は波束とともに動くと考えることができます。
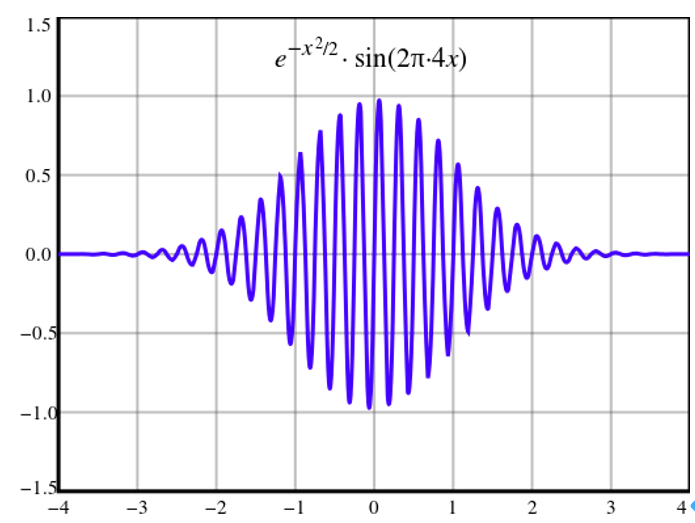
ここで不確定性原理を思い出してください。運動量と位置のどちらかがハッキリするともう一方は全く分からなくなるということでした。この波束は、「運動量と位置のどちらもある程度までわかっている状態」と言えます。そして束縛がないためにこの波束は塊として動いていきます。日常的なサイズ感では実質的にこの波束は粒とみなすことができ、古典力学的と矛盾しないことになります。
光の放出についても考えてみましょう。波束を作っている複数の状態間を連続的に遷移するので連続的なエネルギーの光の出入りを伴います。これがSPring-8内で電場で動かされる電子は連続的な光を放出する理由です。
以上のように、量子力学の波に関する法則で前回提示した「原子の中の電子の謎」は全て説明されるわけです。
| 古典力学から見た原子の謎 | 量子力学による原子の謎の説明 |
| 原子は「すかすか」なのに硬い | 電子軌道のみが電子の許される場所である。不確定性原理により潰されそうになると反発するので硬い。 |
| 原子はつぶれない | 電子は安定な電子軌道の中にあり、原子核にくっつくことはない。 |
| 日常的な大きさの現象では加速した電子は光を出すのに、原子内の電子は運動しても光を放出せずに安定している | 閉じ込められた電子軌道にいる限り光の出入は生じない。一方、束縛されない電子は波束を形成し電場で運動する時に光を放出する。 |
| 原子から出入りする光は決まった「とびとび」の波長のみとなる | とびとびのエネルギーにある軌道間を電子が遷移するときにのみ、軌道のエネルギー差だけの光を吸収・放出する。 |
| 原子は立体構造を持ち互いに決まった角度で化学結合する | 電子軌道は立体構造になる。化学結合とは二つの原子に引かれる電子の軌道のこと。 |
多分、読んだ方は気持ち悪さを抱えたままここまで来たのではないでしょうか。波の共鳴や波束については古典力学でもありますので、気持ち悪さは粒と波の関係のあたりですね。これについては色々な解釈の試みがなされてきました。
次回からは、量子力学の波と粒の関係についてもっと知っていきましょう。いくつかの解釈についても触れていきたいと思います。
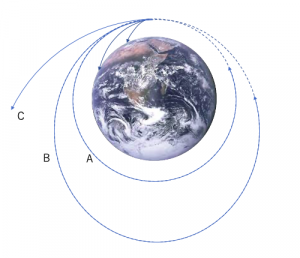
次回: 二重スリット