二重スリット
前回まで原子の中の電子について量子力学の粒と波の関係を見てきました。量子力学の波が一体何であるのかが述べられないまま、波を使って原子の中の電子の動きが説明されたのでスッキリしなかったことと思います。
スッキリしないのは量子力学を専門とする研究者でも同じです。毎日の話題としていくうちに慣れてはいくものの、どこかで心の底から分かったと言いたい願望を持っています。そうして様々に波の性質や考え方が掘り下げられ、量子波動に関する様々な解釈も生まれてきました。
本コラムでは身近な量子力学的存在として原子を最初の話題としましたが、多くのテキストでは「二重スリットを通る電子」を通して量子力学らしさを学ぶことがなされています。
二重スリットは原子に比べると自然界にありふれた状況ではありませんが、量子力学の不思議を語るときに欠かせない共通の話題で、粒と波の関係の奇妙さを最もわかりやすく示しているとも言えます。そこで本コラムでもこの話題を共有し、そこから掘り下げていこうと思います。
さて、スリットとは壁に切れ目が入ったものです。切れ目が一本ならば単スリット、二本なら二重スリットと呼ばれています。スリットの幅は波長程度とします。

音波であれ、水面波であれ、単スリットを通るとき、上から見るとスリットを波源とした円形の波に変わります。スリットから出てきた波の強さをグラフにしたものも合わせて示しておきます。
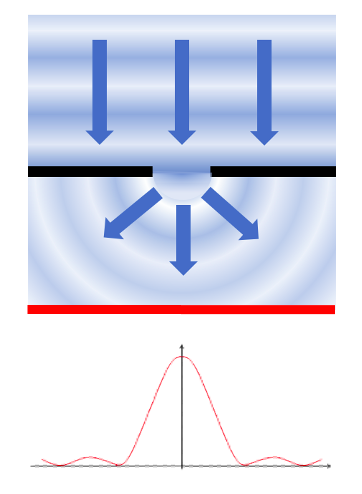
中心に一つの強度の山ができるだけではなく、周辺に小さな山があることにも注意してください。量子力学の入門では話を盛り上げるために無視されがちですが、単スリットでも強度グラフには波のパターンが生まれます。
二重スリットの場合、波源が二つできます。この二つの波源は同じタイミング(位相と呼びます)で揃って動くことがここでのポイントです。その時、二つの波源からの波が重なり合い場所によって激しく揺れるところと、ほとんと揺れないところが生まれます。これが波の干渉と呼ばれる現象です。
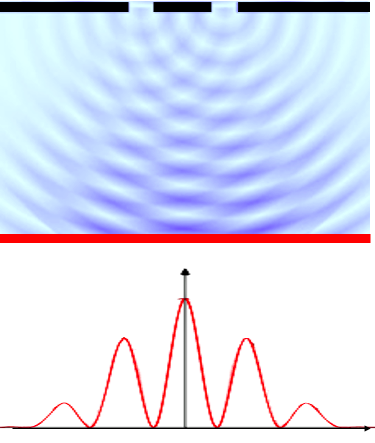
一方、粒の場合どうなるかを考えてみましょう。スリットの上から砂粒を落とします。
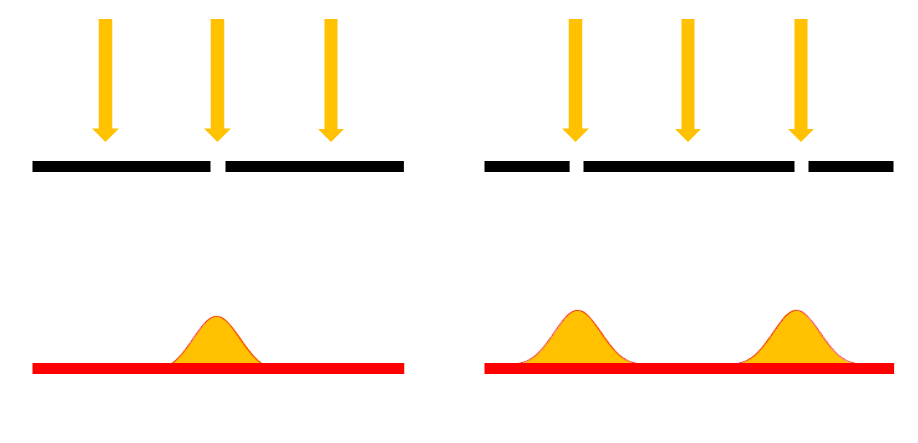
この場合、スリットの先に山ができるだけです。この場合の山の形は正規分布(別名:ガウス分布)と呼ばれています。山の高さを強度グラフとして波の場合と比べると全く異なる結果であることがわかるでしょう。
では、粒と波が両立する量子力学ではどうなるのか見ていきましょう!
電子が当たると跡が残るスクリーンを考え、電子銃からスリットに向けて一定のエネルギーで電子を一つずつ打ち出します。
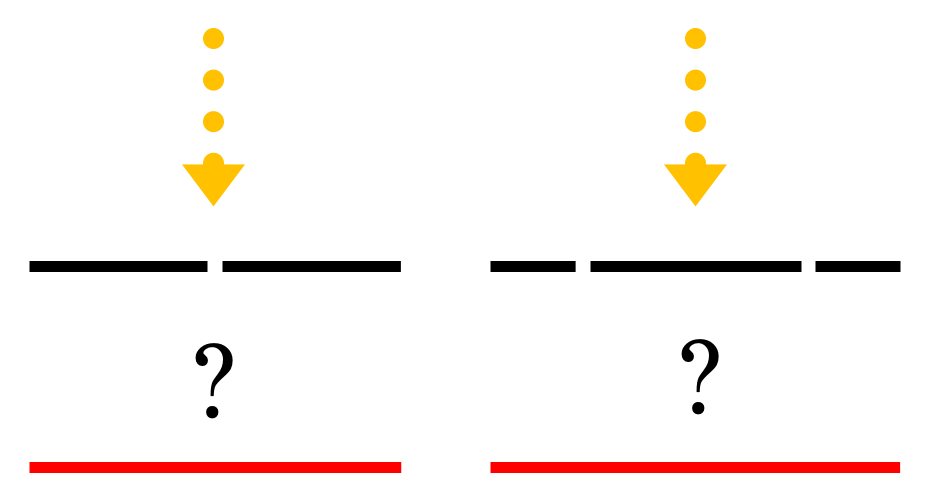
すると、スクリーン上には一つずつ点が記録されていきます。
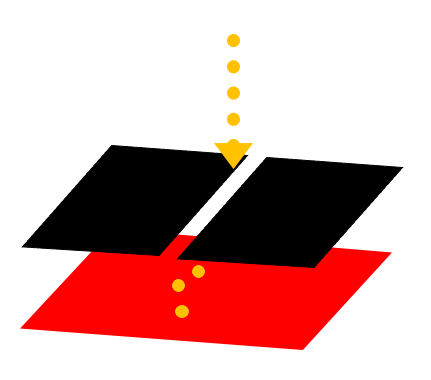
つまり電子は波のように広がったものではなく、あくまでも粒として見つかるということです。
しかし記録を続けていくと・・・。
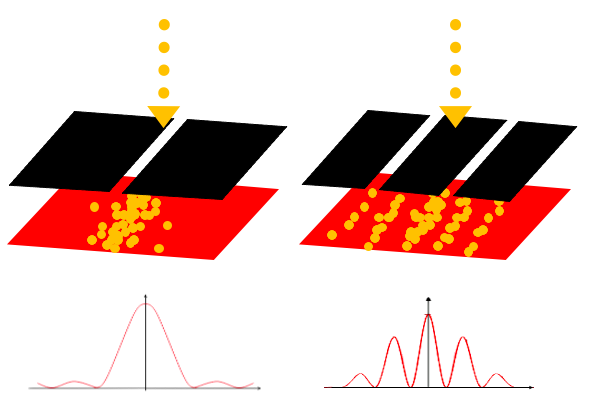
まるで電子は行き先を打ち合わせていたかのように波の強度に従って行き先が振り分けられます。単スリットの結果も正規分布ではなく単スリットの波の強度グラフに従います。以前に「電子を見つける時にはいつでも粒として見つかります。見つかりやすい場所とそうでない場所があり、その確率が波の形をしている」と書いたのはこのことです。
この話の中で、最終的な結果を見るまでは波はありませんでした。電子の発射時も検出時も粒ですから、多分飛んでいる間も粒と思いたいところです。しかしその道のりは波によって決められていたという感じです。
電子一粒ずつが送り出されたわけですから、多数の電子のことを考える必要はありません。一つの電子は「自分自身の波の干渉」によって運ばれ波の形のどこかに一つの計測点を与えます。この実験を繰り返すとやがて波全体の形が見えてきます。
さらに考察を進めてみましょう。二重スリットの一方を閉じると単スリットの結果になります。二つのスリットを波が通り抜けるときだけ干渉はおきますから、波は確実にスリットを二つ通ったわけです。
一方で、 電子が分割できない粒として動き続けているのだとすると、二つのスリットを同時に通り抜けることは不可能です。実際、スリットの近くにスクリーンを置けば電子は必ずどちらか一方のスリットを通ってきたことがわかります。
従って、一方のスリットを開けた状態にし、もう一方のスリットを開け閉めするだけで電子の動きは激変します。複雑な電場をかけた訳でもないのに、その時々で奇妙な曲がり方をして最終的に波を描き出します。
何なんだこれは・・・。でもこれが原子をはじめとする世界の構造に深く関わっている事実なのです。
以上が量子力学の二重スリットの本質です。この話は一つの波長の簡単な波の場合について述べましたが、束縛されていない電子は波束となって進むことを前回述べました。上に説明した二重スリットの話は波束の場合にも成立します。
観測によって波束が消えて粒子になるということからこのテーマは「観測問題」や「波束の収縮」と言われています。量子力学の誕生から現在までこの議論が続く理由はただ一つ、結局この波が何なのか分からないことです。
しかし、量子力学の波は数式で表現され、色々な現象の起こる確率を正しく予言します。まるで、答えを出す手続きはわかっていても仕組みは不明な「完全に当たる占い」のような感じです。
これまで全てを言葉と絵で表現してきましたが、この「量子力学の波」は日常的に目にする波ではないことが分かったと思います。さらに理論上は、量子力学の波は数学でいう複素数でしか表現できないという意味でも普通の波ではありません。
次回は、数学的に量子力学の波がどのように表現されているかをみていきましょう。
次回: 量子力学の波は複素数

若いころに少し学んだ量子力学ですが、大変わかりやすい解説をしていただいているので興味深く拝読しております。
ビジネスでいろいろとお忙しいと思いますが、ぜひとも続きを読ませていただきたく、継続掲載いただければ幸いです。
(Hydro-VENUS様がJ-GoodTechにご登録いただいた関係でこのサイトにやって参りました。)
ありがとうございます。誰も読まないだろうと思っていましたが読んでくださる人がいるのは嬉しいものですね。暇を見つけて継続します。
六十半ばを超え、ふとしたことから量子力学に興味を得ましたが、正直に言って「解らん!」ことばかりです。
大変面白く拝見させて頂きました。ありがとうございます。
是非とも、継続されますようお願いします。
ありがとうございます。仕事で筆が遅いですがまた更新します。