量子力学の波は複素数

普通、私たちがノートなどに波を描くとしたらサインやコサインの波になることが多いのではないでしょうか。横軸が時間や空間で、縦軸は振幅と呼ばれる波の高さですね。（音の場合は高さではなく圧力になります）。

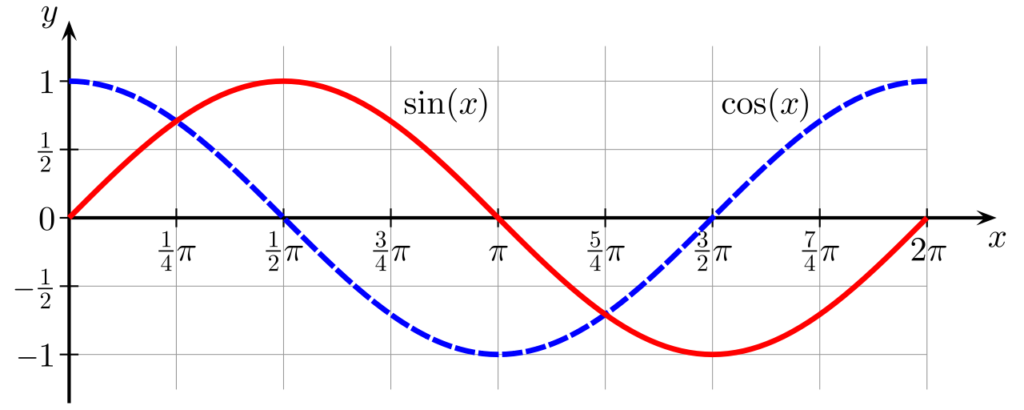
このように一筆書きで滑らかに描く波は実数の波だと言えます。

おさらい：

では量子力学の波が複素数であるとはどういうことなのでしょう？

複素数z=a+biは　実数aと虚数biの和として表現される数です。虚数は二乗すると負の数になるものです。

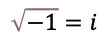
と書けば全ての虚数はiの実数倍で表現できます。

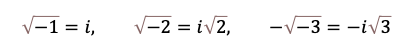
虚数という呼び名が非現実的な印象を与え、それを含む複素数は直感的にわかりにくいことと思います。しかし、以下に示すように虚数の意味と世界観が理解できるとそれを使って表現される景色自体はそれほど手強くはないと思ってもらえるはずです。

まず、あまり深く考えずにルールとして受け入れて来た人が多そうな話題から始めます。

マイナス掛けるマイナスがプラスになること：

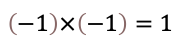
とはどういう意味でしょうか。

負の数は正の数から見てゼロの向こう側にあります。これはプラスの数に対して鏡の向こうにある反転世界（負数の世界）を考えることを意味します。

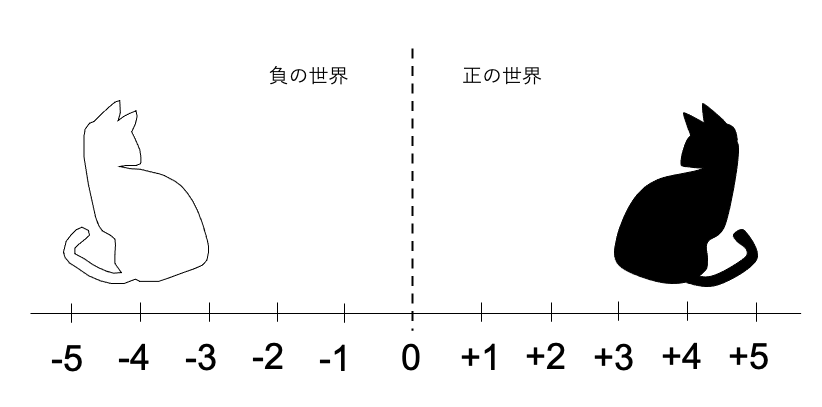
また、３から１減ることは3-1と表現できますが、増える方向を前向きとした時に３歩進んだあとに「反転して」一歩進むと考えることができます。

このように、マイナスとは反転操作が関係しています。マイナス掛けるマイナスがプラスになるのは反転を２回繰り返すと元の向きに戻ることと理解することができます。

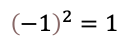
このように”ー（マイナス）”という操作によってゼロの向こう（反転方向）に延長した世界を作っているわけです。

では虚数とは何でしょうか。平方根は指数で表現すると1/2乗ですから以下のように書けます。

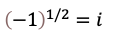
言い換えるとマイナス（反転）の半分の操作がiです。完全に振り返るちょうど途中には横を向いている・・・虚数は90度回転操作・・・と考える世界観が虚数であり、虚数によって広がった世界が複素数です。

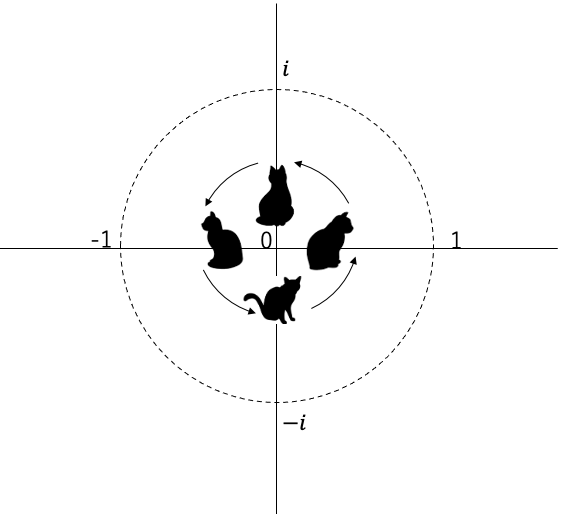
これも新たな操作iによって直交（90度回転）した方向に延長した二次元世界を作ったわけです。実軸と虚軸で作られる複素平面で表現され、この平面上の全ての数は実数と虚数で表すこともできますし、中心からの距離と角度でも表現できることになります。

このように考えると、虚数は90度回転した方向を向く操作であり、マイナスは180度回転した方向を向く操作として統一的に見ることができます。虚数や複素数を現実にないものではなく、回転するものを簡潔にうまく表現する手段と捉えることがここでのポイントです。

そして、そのような観点に基づいて

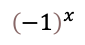
のxを実数にして滑らかに変化させることを考えましょう。それは複素平面上で滑らかに回転することを意味します。

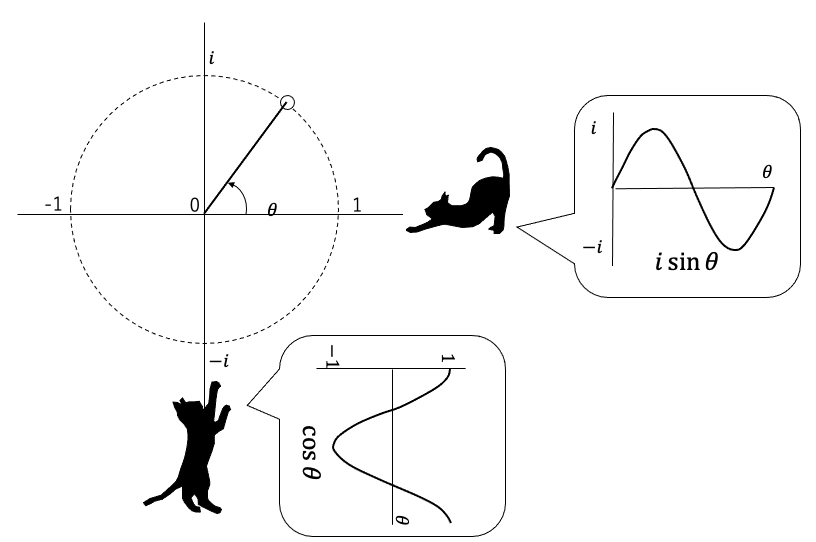
そして上の図からもわかるように次のように表現できます。

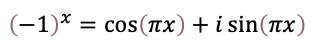
ここで冒頭で触れたサインとコサインが現れました。回転を実軸に投影したものがコサインで虚軸に投影したものがサインとなります。波は回転運動を一方向からみたものと言えます。

通常は、オイラーが導いた関係

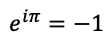
で上に書いた式の-1を置き換えて以下のように書きます。

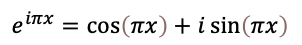
あるいはπxを角度θ（位相と呼びます）で書き直して

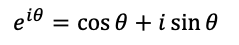
と書かれます（オイラーの公式）。eはネピアの数です。

上記を空間と時間で表現してみましょう。空間的な繰り返し単位が波長（λとします）、時間的な繰り返し単位を周期（Tとします）として

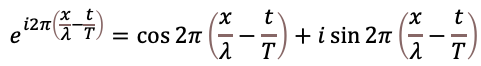
となります。

これが量子力学の「波動関数」の基本形となります。私たちは基本的に回転の話をしてきましたが、右辺の実軸と虚軸のサインとコサインそれぞれは代表的な波の関数であることや、空間上をこの位相回転が伝わっていく様子の表現としてこれを複素数の波と呼んでいます。

上の式は少し複雑になりましたが内容はそれほど難しくありません。xがλの定数倍に変化するたび、またtがTの定数倍に変化するたびにθが2π変わって複素平面上の元の状態に戻ります。

ついでに位相θ=0である点がどのように動くかをみてみましょう。

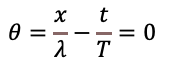
整理すると

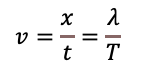
波長と周期は一定ですからこの点は一定速度vで進んで行きます。

上記の説明を通して伝えたかったのは次のことです。

• 現実世界にありふれた回転の表現として複素数を捉えることができる
• 波は回転の一部を取り出したもの（縦軸と横軸に投影したもの）と捉えることができる

一般に思われているほど虚数や複素数は不可解なものではありません。また、「複素数の波」という難解な表現は「位相の回転が波のように伝わる」という程度に考えても良いように思います。（別の回でこの波動関数を確率に関連づけるときに確かに波形が現れることがあることを説明します）

波であれ回転であれ、θが一周すると状態が元に戻るのがここでの本質で、飛行する電子一つとっても空間と時間の上で位相がぐるぐる回るのが量子力学の重要な特徴です。

量子力学では確かに「波と呼ばれている何か」が現象を支配しているのですが、上記の見方で言えば「微小世界に特徴的な循環現象」を取り扱っていると言えるかと思います。

量子力学の波の正体がよく分からない事実は、このミクロな世界の循環の正体が未だ分からないと言い変えることができるかもしれません。

最後に量子力学では位相が運動と関係してどのように回転するのか見てみましょう。

一定の運動量とエネルギーを持って自由に空間を飛行する粒子を考えましょう。量子力学では波ψの波長λや周期Tが運動量pとエネルギーEに以下の法則で関係づけられます。ここでは簡単のため１次元の位置xと時間tで表現しています。

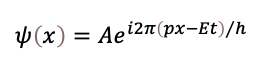
hはプランク定数という量子力学の最も重要な定数です。なお、Aは比例定数ですが、どちらかというと辻褄が合うように調整される因子となります。量子力学にとって本質的に大事なのは位相なのです。

上に示した波の式と比較して以下が確認できます。

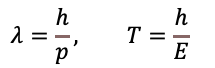
第一の式はド・ブロイによって与えられた物質波（微小な世界では運動するあらゆる物質は運動に応じた波長の波を伴う）の表現になっており、後者は周期Tを振動数ν=1/Tで書き換えると

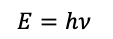
となって、プランクによって見出されたエネルギー量子（微小な世界ではエネルギーが連続ではなく振動数で決まるとびとびの値になる）の表現になっています。

電子などが空間中で場の影響を受けずに自由に飛んでいるときはこの例のように運動量やエネルギーは一定ですが、場があると加速されたり減速されたりして変化します。そのとき、波の波長や周期も変化することになります。あるいは位相の回転が加速したり減速したりするわけです。

一般に運動量やエネルギーが大きいほど位相回転も激しくなります。

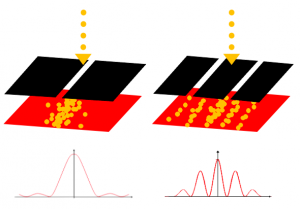
前回の「二重スリット」の解説の中で、電子が動いているときにだけ波があり、観測されて動きが止まると波が消える「波束の収縮」を紹介しました。上記の式を見れば運動が失われると位相がゼロになり回転も波も確かになくなることがわかります。この運動量とエネルギーに関係した位相の循環が空間を伝達し二重スリットを通り抜けたわけです。

ところで、電気工学などでも波を複素数で表すことがありますが、それは計算の便利さのためで本質的には実数でも表現できます。しかし量子力学の場合は複素数でないと表現できない事実があります。今回お話ししたように、波であることよりも循環があることが本質と言えるように思います。

次回は、量子力学の波の形を決めている法則（シュレーディンガー方程式）を示し、実数ではなく複素数でないと理解できない現象の例としてトンネル効果を紹介します。

次回：　シュレーディンガー方程式